「シンガポール式算数」という新しい算数メソッドが世界中で注目を集めています。
世界中の小学生・中学生の算数/数学と理科の学力調査TIMMSで、1995年からトップを続けているのがシンガポールです。シンガポールの小中学生の好成績を支えているシンガポール式算数メソッドは、シンガポールや上海だけでなく、アメリカやカナダの教科書にも取り入れられるなど、広がりを見せています。アマゾンの創設者であるジェフ・ベゾスが、お子さんをシンガポール算数を学ぶキャンプに参加させたという報道もあります。
本記事ではシンガポール式算数とはどのようなものか、そのメリットも含めて説明します。また、日本で学ぶ方法などもあわせて紹介します。
1. シンガポール式算数とは
シンガポール式算数の大きな特徴は以下の2点です。
2. 文章題は視覚的に把握しやすいバーモデルを使う
実際に問題を見ながら、シンガポール式算数の特徴を見てみましょう。
(※以下の問題は小学校1年生向けの問題を元に、ちいくば編集部で作成しています)
Q1. かごの中にりんごとみかんが全部で10個入っています。みかんはりんごより2個多いです。りんごとみかんはそれぞれいくつあるでしょう?

A1. バーモデルでは上記のように、基本となる「まとまり」を「1ユニット」として考えます。このユニットと他の数字を関連づけていきます。
ここではりんごの個数を1ユニットととらえます。みかんは1ユニット+2個です。
2ユニットだと、10個-2個=8個
そこで1ユニットが4個であることがわかります。
これを「1年生から?」と驚かれる方もいらっしゃるかもしれません。
シンガポールでは掛け算や割り算を習うのは小学校2年生からですが、1年生であっても、普段から以下のように数に慣れるトレーニングを重ねています。
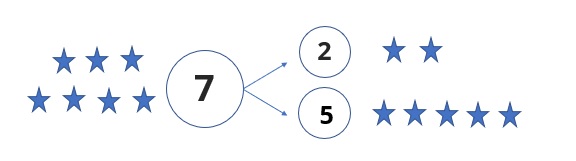
これは「足したら7になるペアを見つけましょう」という設問です。星や本など身近な具体物を使って、色を塗りながら数の組み合わせを学びます。そのため割り算を習っていなくても、8が「4と4で同じ数のペアである」ことが理解できているのです。
バーモデルと線分図の違い
上記の例題を見て、中学受験をご存じの方はすぐに「これは和差算だな」と思われることでしょう。学校でも小学校4~5年生で同様の文章題は習いますが、「和差算」という言葉は使いません。
日本では、このような問題は線分図を使って解きます。
Q2. 太郎君は本屋でマンガと本を買い、1,080円を払いました。マンガより本は120円高かったです。マンガと本はそれぞれいくらだったでしょう?

A2. 線分図を使って解く場合、本のでっぱりの部分を除いた2つの線分の長さが同じであることに着目し、本のでっぱりを除くか、マンガの値段に120円を加えてやるかのどちらかの方法で答えを出します。ここでは除いた計算を使います。
(1080-120)÷2=480(円) …マンガの値段
480+120=600(円) …本の値段
このように線分図は問題に出てくる数字を視覚的に把握できる優れた手段です。ただ、線分図で扱えるのは足し算・引き算および倍数で使える場合で、和差算、年齢算、倍数算など使える文章題の種類も限られています。積に注目する文章題である食塩水やつるかめ算などでは面積図を使います。
そのため「どちらを使ったらよいのかわからない」と迷う子どもも出てきます。
しかし、バーモデルは「何をユニットに置くか」が基本になっているため、図形や速度の問題にも応用して使うことができます。
問題が複雑になれば、バーモデルでは解けない文章題も出てきますが、バーモデルをしっかりと学ぶことによって、複雑な問題にも対応できるようになります。
日本の算数教育の現状
日本での算数・数学のカリキュラムもまた、よく考えられたものです。小中学生を対象とした国際比較調査TIMSSでは、4年ごとに小・中学生の算数(数学)・理科の学習到達度のテストを行い、調査結果を公開しています。
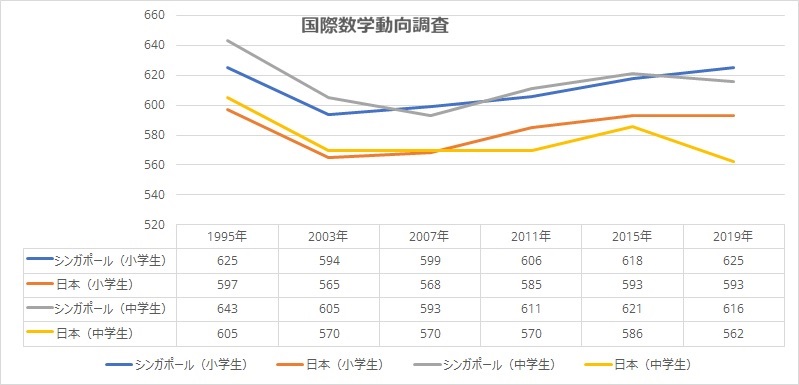
以下はその結果の中から、日本とシンガポールの成績を表したグラフです。
TIMSSには年度によって違いがありますが、おおよそ世界50か国近い国と地域が参加しています。シンガポールや韓国、台湾、香港、日本などアジア地域が上位を独占しており、中でもシンガポールは小学校算数では2007年、中学数学では2007年と2011年を除けば、1位を獲得しています。
日本もシンガポールや韓国、台湾、香港に次ぐ順位を占めており、国際的には高い水準であるといえるでしょう。
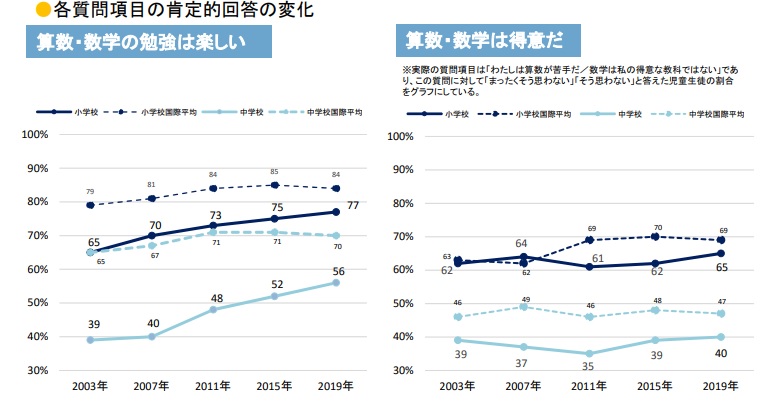
算数・数学が「得意」と思えない日本の子どもたち
国際的に見て、高い水準を占めている日本ですが、大きな特徴があります。算数・数学の勉強が「楽しい」「得意だ」と答える子どもの割合が、国際平均に比べても低いのです。
高い成績を上げているのに「楽しい」と感じている子どもが少なく、苦手意識を抱いている背景には、「このくらいの点数で得意だなんて言えない」という、日本人特有の心理的傾向もあるでしょう。
しかし同時に日本の算数教育が「考える楽しさ」や「達成感」を十分に与えていないと言えるのではないでしょうか。
シンガポール式算数を学ぶメリットと標準的教育の違い
シンガポール式算数を学ぶメリットとして、以下の2点を挙げることができます。
- 自分で考える習慣がつく
- 達成感を味わえる
日本を含め、多くの国での標準的な授業の進め方は、まず先生が問題の解き方を説明し、子どもたちはそれと同じやり方で問題を解く、というものです。それからその例に近い問題を解き、数や条件を少しずつ変えた問題を、同じ手順で繰り返して解きます。
効率的に問題が解けるようになるには良い方法ですが、反面「わかる」ことよりも「できるようになる」ことを重視しすぎると、「できるけれども楽しくない」「できるけれども自信につながらない」ことになりかねません。
一方、シンガポール式算数は、最初にバーを書いたり、色を塗ったりするなど視覚的な要素を用いた作業を行いながら、自分で考えを深めることから始めます。すでにあるやり方をなぞるのではなく、自分で試行錯誤しながら進むため、思考力と達成感が養われます。
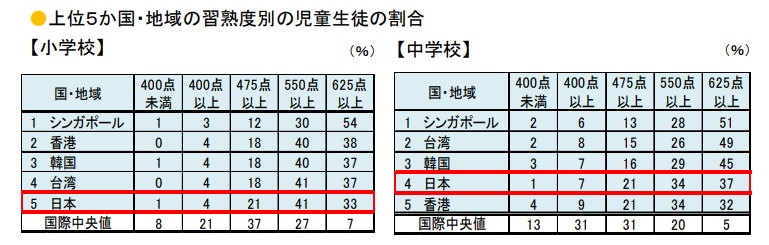
その結果、1つ問題が解けるようになると、もっと難しい問題に取り組もうとする意欲が生まれます。シンガポール式算数でこの好循環が生まれる根拠となる調査結果がこちら↓
上の表は、TIMSS上位国の習熟度別に子どもたちの割合を比較したものです。
日本の小学校では、中位~中上位に多くの子どもたちが集中するのに対し、シンガポールでは上位層がとびぬけて最も多くなっています。
標準的な問題を解ける基礎力はあるのに、難しくなると考えるのを止めてしまう子どもたちと(日本)、難しい問題に主体的に取り組む子どもだち(シンガポール)の差が、この結果に表れているのではないでしょうか。
日本でシンガポール式算数を学ぶには?
アメリカやカナダでは、公教育でもシンガポール式算数を取り入れているところが増えていますが、残念ながら現時点では日本の公教育では取り入れられていません。しかし、シンガポール式算数を導入した教授法の研究は行われており、将来的には導入されるかもしれません。
現在、手軽にシンガポール式算数を学ぶ手段としては、本を使って問題を解きながら学ぶ方法があります。
学年別のドリル形式になっており、習熟度合いに合わせて進むことができます。
本記事で紹介したバーモデルだけでなく、パズル要素の高い問題なども紹介されているため、大人でも楽しむことができます。
さらに興味を持たれた方は、英語版になりますが、Singapore Math Inc.のサイトから購入することもできます。英語といってもビジュアルが中心で子ども向けなので、英語が得意でない方でも内容を理解する妨げにはなりません。

ビジュアルも豊富で楽しいテキストです。英語の勉強も合わせて行いたいという方は、ご検討ください。
「算数が好き」「算数が得意」と思える子どもたちに
シンガポール式算数のすばらしい点は、何よりも「じっくり考える」「自分で考えて答えを導き出す」という点にあります。
日本ではシンガポール式算数を体系的に学べる場所が限られているため、シンガポール式算数を学び続けるには家庭学習が中心になります。
しかし、小学校の低学年のうちにシンガポール算数の基礎であるバーモデルやパズルを楽しむだけでも、数と数の関係に対する感覚が養われ、その後、大きな強みになるでしょう。